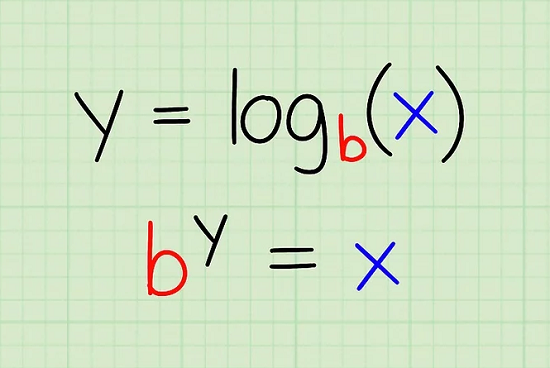What is the value of this sum?

\[\frac{1}{log_{2}(100!)} + \frac{1}{log_{3}(100!)} + \frac{1}{log_{4}(100!)} + \ldots + \frac{1}{log_{100}(100!)}\]

Well, it turns out that the answer is just \(1\). Isn’t that cool. Let’s prove it.

Prep

Let’s recall some basic logarithmic identitities. First the relationship between logs of different bases …

\[\log_{b}(a) = \frac{log_{c}(a)}{\log_{c}{b}}\]

And then the relationship between the log of the product of two numbers and the logs of those numbers …

\[\log(ab) = \log(a) + \log(b)\]

Proof

We are asked to show that …

\[\frac{1}{log_{2}(100!)} + \frac{1}{log_{3}(100!)} + \frac{1}{log_{4}(100!)} + \ldots + \frac{1}{log_{100}(100!)} = 1\]

We know that …

\[\log_{b}(a) = \frac{log_{c}(a)}{\log_{c}{b}}\]

So …

\[\log_{2}(100!) = \frac{log(100!)}{\log{2}}\]

Where \(log\) here represents log to the base \(e\).

Therefore …

\[\frac{1}{\log_{2}(100!)} = \frac{\log{2}}{log(100!)}\]

Similarly …

\[\frac{1}{\log_{3}(100!)} = \frac{\log{3}}{log(100!)}\] \[\frac{1}{\log_{4}(100!)} = \frac{\log{4}}{log(100!)}\] \[\dots\] \[\frac{1}{\log_{100}(100!)} = \frac{\log{100}}{log(100!)}\]

So the left hand side of the original expression is …

\[\frac{log(2) + log(3) + log(4) + \ldots + \log(100)}{log(100!)}\]

We also know that …

\[\log(a) + \log(b) = \log(ab)\]

So …

\[log(2) + log(3) + log(4) + \ldots + \log(100) = \log(2 \cdot 3 \cdot 4 \cdot \ldots \cdot 100) = \log(100!)\]

Plugging this back into the left hand side of the original expression we get …

\[\frac{\log(100!)}{\log(100!)}\]

Which is equal to \(1\). Therefore …

\[\frac{1}{log_{2}(100!)} + \frac{1}{log_{3}(100!)} + \frac{1}{log_{4}(100!)} + \ldots + \frac{1}{log_{100}(100!)} = 1\]

QED