Proof. An interesting word with several meanings …

noun

• Evidence or argument establishing or helping to establish a fact or the truth of a statement
• A trial print of something, in particular
• A measure of the content of ethanol in an alcoholic beverage

adjective

• Able to withstand something damaging; resistant
• Denoting a trial impression of a page or printed work

verb

• Make (fabric) waterproof
• Make a proof of (a printed work, engraving, etc.)

Although I very much like the third noun usage, today we are going to be discussing proof in the context of mathematics and in particular, the various forms in which it can be achieved.

The Mathematical Edifice

I like to think of mathematics as a structure and a tall and impressive one at that, which only ever gets taller over time. Each level of the structure builds on the layers below and at the very bottom is a foundation upon which everything depends. These foundations are known as axioms things which are assumed to be true and require no proof of themselves. Above the axioms are theorems, statements which are shown to be true based on the logical application of the axioms and theorems that lie below them. The truth of each level of the structure depends on the truth of the layers below. In any lower level theorem is proven to be false then the truth of all the theorems above is thrown into doubt.

Geometry is a classic example of an edifice built on a set of axioms where the type of structure that you end up with depends critically on which axioms are assumed and not assumed, the so called parallel postulate being a ready example. Eucliden Geometry is the study of geometry that satisfies all of Euclid’s axioms, including the parallel postulate. A geometry where the parallel postulate does not hold is termed non-Euclidean and there are several types thereof (hyperbolic, elliptic, etc.)

The process of building the edifice depends wholy on the nature of mathematical proof.

Mathematical Proof

Formally, in mathematics, a proof is an inferential argument for a mathematical statement. In the argument, other previously established statements, such as theorems, can be used. In principle, a proof can be traced back to self-evident or assumed statements, known as axioms, along with accepted rules of inference. Axioms may be treated as conditions that must be met before the statement applies. Proofs are examples of exhaustive deductive reasoning or inductive reasoning and are distinguished from empirical arguments or non-exhaustive inductive reasoning (or “reasonable expectation”). A proof must demonstrate that a statement is always true (occasionally by listing all possible cases and showing that it holds in each), rather than enumerate many confirmatory cases. An unproved proposition that is believed to be true is known as a conjecture. Proofs employ logic but inevitably include some amount of natural language which can admit some ambiguity. In fact, the vast majority of proofs in written mathematics can be considered as applications of rigorous informal logic.

Pause. Breathe.

Informally, proofs are things that are required in order to pass examinations in mathematics but which many students consider not that important in the grand scheme of things and sometimes even a load of dingo’s kidneys.

The presentation of a mathematical proof generally follows a format. The proposition to be proved is first stated along with any related assumptions about the elements involved in the proposition. What follows is a logical progression of statements, the truth of each of which is inferred from the statements that came before it coupled with other things (definitions, axioms and theorems) that we already know to be true. This progression of true statements proceeds until the original proposition is stated, at which point the proof is complete. Finally, and traditionally, the term QED appears which is an acronym for the Latin phrase quod erat demonstrandum meaning “what was to be demonstrated” or “what was to be shown”. An alternative, although slightly inaccurate, translation is “thus it has been demonstrated”.

Types of Proof

Mathematical proofs fall into various categories. Each of these can be considered an approach to a proof, or a tool that can be employed in pursuit of a proof. Many theorems can be prooved in different ways using different techniques. For example, the classic theorm of Pythagoras is said to have at least 370 known distinct proofs.

Proof by Deduction

A proof by deduction is a technique in which the succession of true statements is achieved via deductive reasoning. We proceed from statement A to statement B via an implication inferred from the assumed truth of A conjoined with other known truths (definitions, axioms and theorems).

The direction of the implication of truth between two statements must be carefully considered. For two related statements A and B we can have.

A if B

• “B is true” implies that “A is true” (B => A)
• “A is false” implies that “B is false” (!A => !B)
• This is the same as B only if A

A only if B

• “B is false” implies that “A is false” (!B => !A)
• “A is true” implies that “B is true” (A => B)
• This is the same as B if A

A if and only if B

• “A is true” implies that “B is true” (A => B)
• “A is false” implies that “B is false” (!A => !B)
• “B is true” implies that “A is true” (B => A)
• “B is false” implies that “A is false” (!B => !A)

• The two statements are logically equivalent (A <=> B)

• Example 1:*

• Statement A: x > 10
• Statement B: x > 5

B if A (equivalently A => B) but not A if B. B does not imply A. E.g. x = 6 satisfies B but not A.

Example 2:

• Statement A: n is an even number
• Statement B: n = 2k for some integer value k

A if and only if B (equivalently A <=> B)

Proof by Induction

A proof by induction is just like an ordinary proof in which every step must be justified. However, it employs a neat trick which allows you to prove a proposition about an arbitrary positive integer n by first proving it is true when n = 1 and then assuming it is true for n = k and showing (via other deductive reasoning) that it is also true for n = k + 1. By doing this we can then say that since the proposition is true for n = 1 then it must also be true for n = 2 (since true for k implies true for k + 1); and since it’s true for n = 2 then it must also be true for n = 3 and so on and so forth ad infinitum. Thus the proposition must be true for all positive integer values of n.

Proof by Contradiction

Proof by contradiction starts out by assuming that the opposite of the proposition is true, and then shows that such an assumption leads to a contradiction. Thus the original assumption (that the proposition is false) cannot be true and so we can deduce that the proposition must be true. This style of proof is a particular kind of the more general form of argument known as reductio ad absurdum.

G. H. Hardy described proof by contradiction as “One of a mathematician’s finest weapons”, saying “It is a far finer gambit than any chess gambit: a chess player may offer the sacrifice of a pawn or even a piece, but a mathematician offers the game.”

Other

Other styles of proof exist, such as proof by construction and proof by exhaustion but the main tools in a mathematician’s toolbox are those outlined above. Another style, although not formal, is the visual proof or proof without words. A great example of this would be the following visual representation of Pythagoras’ Theorem.

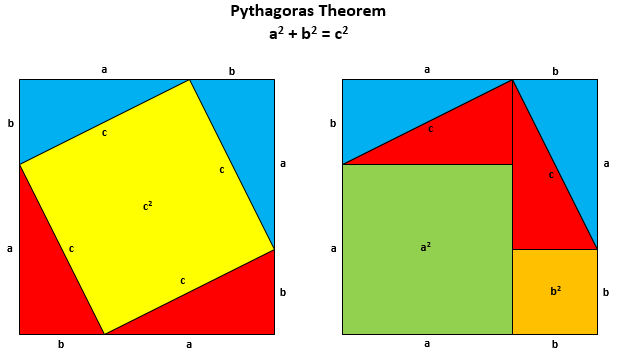
Example Proofs

Let’s consider some interesting mathematical propositions and then use the different types of proof to turn those propositions into theorems.

1089

I’m not sure if this one counts as a theorem but it’s a fun mathematical trick that we can demonstrate to be true via deductive reasoning based on the initial conditions.

Proposition …

Pick any three digit positive decimal integer where the first digit is greater than the last. Reverse the digits to form another positive three digit integer and subtract this new integer from the first. The result will be another three digit positive integer. Reverse the digits of this new number and then add the resulting number to the result from the first operation. The answer will be 1089 and will always be 1089 regardless of the initial choice of number.

Examples …

• \(N = 321\); \(N_{rev} = 123\); \(N - N_{rev} = M = 198\); \(M_{rev} = 891\); \(M + M_{rev} = 1089\)
• \(N = 780\); \(N_{rev} = 087\); \(N - N_{rev} = M = 693\); \(M_{rev} = 396\); \(M + M_{rev} = 1089\)
• \(N = 500\); \(N_{rev} = 005\); \(N - N_{rev} = M = 495\); \(M_{rev} = 594\); \(M + M_{rev} = 1089\)

Proof (by deduction) …

Let’s assume that the digits of our initial number, \(N\), are \(a\), \(b\) & \(c\).

We know: \(a \in [1, 9]\), \(b \in [0, 9]\), \(c \in [0, 9]\), \(a > c\) and \(N = 100a + 10b + c\).

We know that \(a\) cannot be zero because \(a > c\).

Now, \(N_{rev} = 100c + 10b + a\) and therefore \(N - N_{rev} = M = (100a + 10b + c) - (100c + 10b + a)\).

Simplifying, we have \(M = 100a - a + 10b - 10b - 100c + c = 99a - 99c = 99(a - c)\).

We know from our initial assumptions that \(a - c > 0\) and \(a - c \in [1, 9]\) so \(M\) is a positive multiple of \(99\) and further, \(M \in \{ 099, 198, 297, 396, 495, 594, 693, 792, 891, 990 \}\).

For each of these possible values of \(M\), the middle digit is \(9\) and the first and last digits sum to give \(9\). If we write the digits of M as \(a\), \(9\) & \(c\) then …

\[M + M_{rev} = (100a + 90 + c) + (100c + 90 + a) = 100(a + c) + 180 + a + c\]

But we know that \(a + c = 9\) and therefore \(M + M_{rev} = 900 + 180 + 9 = 1089\).

QED

A Formula for the Sum of the First N Positive Integers

Proposition …

\(1 + 2 + 3 + 4 + ... + n = \frac{n(n + 1)}{2}\) for all positive integers \(n\).

Proof (by induction) …

Assume that the proposition is true for \(n = N\). So we can take this as true …

\[1 + 2 + 3 + 4 + ... + N = \frac{N(N + 1)}{2}\]

Add \(N + 1\) to both sides to give …

\[1 + 2 + 3 + 4 + ... + N + (N + 1) = \frac{N(N + 1)}{2} + (N + 1)\]

We can rearange the right hand side to give …

\[\frac{N(N + 1)}{2} + (N + 1) = \frac{N(N + 1) + 2(N + 1)}{2} = \frac{N^2 + 3N + 2}{2} = \frac{(N + 1)(N + 2)}{2}\]

and so …

\[1 + 2 + 3 + 4 + ... + N + (N + 1) = \frac{(N + 1)(N + 2)}{2}\]

which is the same as the original proposition but with \(n = N + 1\).

So the proposition being true for \(n = N\) logically implies it is also true for \(n = N + 1\).

It is trivially true for \(n = 1\) since \(1 = \frac{1(2)}{2}\) is true.

Therefore it must also be true for \(n = 2, 3, 4, ...\).

Therefore it is true for all positive integers.

QED

The Infinitude of the Primes

Definition: A prime number is a positive integer that is only evenly divisible by itself and one.

Proposition …

There are infinitely many prime numbers.

Proof (by construction/induction) …

Let’s take any finite set of prime numbers \(\{p_1, p_2, p_3, ..., p_n\}\) and then let’s form the number \(N = (p_1 \times p_2 \times p_3 \times ... \times p_n) + 1\).

\(N\) must have a prime factor but that factor can’t be any of \(\{p_1, p_2, p_3, ..., p_n\}\) because, by construction, there will always be a remainder of \(1\) when \(N\) is divided by any of the primes in our set.

Therefore there must be another prime that is not in our set.

But we chose our initial finite set of primes arbitrarily. Thus for any finite set of primes there must be another that is not in the set.

Therefore there are infinitely many prime numbers.

QED

The Irrationality of the Square Root of Two

Definition: A rational number is one that can be expressed as the quotient \(\frac{p}{q}\) of two integers, a numerator \(p\) and a non-zero denominator \(q\). An irrational number is a real number that is not a rational number.

Proposition …

The square root of two is an irrational number.

Proof (by contradiction) …

Assumption: \(\sqrt{2}\) is rational

Thus \(\sqrt{2}\) can be expressed as \(\frac{p}{q}\) where \(p\) and \(q\) are integers with no common factors (other than \(1\)) and where \(q\) is non-zero.

\(\sqrt{2} = \frac{p}{q}\) therefore \(2 = \frac{p^2}{q^2}\) and so \(2q^2 = p^2\)

Thus \(p^2\) must be an even number since it is an integer multiple of \(2\).

Now, if \(p\) was odd, i.e. \(p = 2k + 1\) for some integer \(k\) then \(p^2 = (2k + 1)^2 = 4k^2 + 4k + 1\) which is also odd. If \(p\) was even, i.e. \(p = 2k\) for some integer \(k\) then \(p^2 = (2k)^2 = 4k^2\) which is also even. So \(p^2\) odd <=> \(p\) odd and \(p^2\) even <=> \(p\) even.

So, \(p\) is even, i.e. \(p = 2k\) for some integer k.

Substituting this back into \(2q^2 = p^2\) gives \(2q^2 = (2k)^2 = 4k^2\) and thus \(q^2 = 2k^2\) which means that \(q^2\) is even as well (since it’s a multiple of \(2\)) and so, by the same argument as above, \(q\) must be even too.

So, \(p\) and \(q\) are both even.

But this contradicts our initial assumption that \(p\) and \(q\) have no common factors other than \(1\). Thus our initial assumption must be false and so \(\sqrt{2}\) can’t be rational. Thus it is irrational.

QED