The Question
This post is inspired by a question that I was asked in an interview once. Here it is …
Assume that you have an unordered binary tree where the values stored at the nodes are positive integers. Write code to find the length of the longest path through the tree that consists of nodes whose values are in strict increasing or decreasing order. A path proceeds from node to node via the obvious parent-child relationships and can go up and down.
An example is in order. In this tree …
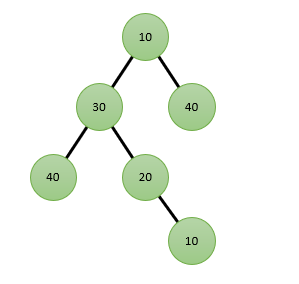
… the longest path is of length four. The path is [10, 20, 30, 40] (starting from the lowest 10 node, proceeding up to the 30 node and then down to the lowest 40 node). We could also list this path in descending order, the order of traversal doesn’t matter.
Solution Strategies
So how would we go about solving this for a general binary tree? Well, most tree algorithms involve some sort of recursive traversal while maintaining state. The traversals are pretty generic, it’s the state you track along the way and how you use that state that will be key.
Binary Tree Traversals
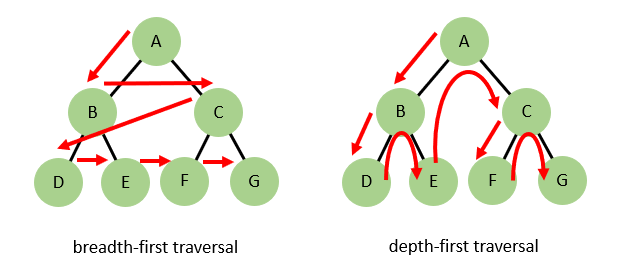
There are various types of tree traversal. The first distinction is between breadth-first and depth-first. In the former the tree is fully explored left to right at each level before proceeding to the next level, whereas in the latter the tree is fully explored root to leaf by following the left child at each node before then jumping up and following the right node.
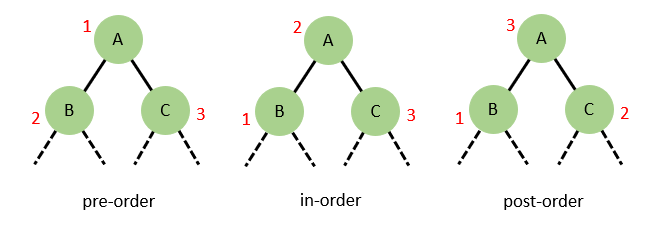
With a depth-first search there are three further types of traversal based on the order in which the root node and children (sub-trees) of a given tree are processed. These are pre-order (the root is processed first then the children), in-order (the left is processed first, then the root, then the right) and post-order (the children are processed first and then the root).
Generic Code for Tree Traversal
To solve this problem we are going to need a depth-first, post-order traversal, i.e. one where we process all the children before we process the root. This represents an exhaustive, bottom up search. Let’s write some code to do that.
namespace GinjaSoft.TreeStuff
{
using System;
public class Node<T>
{
public Node(T value) { Value = value; }
public T Value { get; set; }
public Node<T> Left { get; set; }
public Node<T> Right { get; set; }
}
public static class BinaryTreeTraversals
{
public static void DepthFirstPostOrder(Node<T> root, Func<Node<T>, TResult, TResult, TResult> fn)
{
TResult leftResult = default;
TResult rightResult = default;
if(root.Left != null) leftResult = DepthFirstPostOrder(root.Left, fn);
if(root.Right != null) rightResult = DepthFirstPostOrder(root.Right, fn);
return fn(root, leftResult, rightResult);
}
}
}
This is a generic code. What we actually “do” at each node is factored out into a function that the client code will supply. This function has to adhere to a given prototype, it needs to take three parameters (a reference to the node to process and two instances of a result type - that will be generated from the processing of the left and right children respectively) and it needs to return a result type that will represent the result of processing the node.
Specific Code for the Problem at Hand
Here’s how we might write some client code to use the generic traversal code. First we need to define the result type (TResult) that will represent the result of processing a node. This type will be used to hold information about the paths that exist in each sub-tree within a tree as we recursively traverse all the nodes in a depth-first post-order manner.
namespace GinjaSoft.TreeStuff
{
public partial class LongestPath
{
//
// This type contains information about the paths that exist within a given sub-tree
//
public class NodeInfo
{
// The value of the tree's root node
public uint RootValue { get; set; }
// The length of the longest path of nodes (up through the root) with consecutively increasing values
public uint MaxIncPathLenToRoot { get; set; }
// The length of the longest path of nodes (up through the root) with consecutively decreasing values
public uint MaxDecPathLenToRoot { get; set; }
// The length of the longest path of nodes with either consecutively increasing or decreasing values.
// This path does not have to include the root node and also doesn't have to extend exclusively up the
// tree towards the root. The path can start from a given node, proceed upwards through other nodes
// and then downwards again through child nodes. This is the value of interest.
public uint MaxPathLen { get; set; }
}
}
}
Here’s how we’ll use this type with the DepthFirstPostOrder method …
namespace GinjaSoft.TreeStuff
{
public partial class LongestPath
{
//
// This function is the solution to the interview question
//
public static uint GetMaxPathLength(Node<uint> tree)
{
var nodeInfo = GetNodeInfo(tree);
return nodeInfo.MaxPathLen;
}
//
// Implementation
//
internal static NodeInfo GetNodeInfo(IBinaryNode<uint> tree)
{
// Unfortunately I can't pass ProcessNode directly to DepthFirstPostOrder. C# won't do the implicit
// cast from method group to Func and so a local variable is required. Sigh.
Func<Node<uint>, NodeInfo, NodeInfo, NodeInfo> fn = ProcessNode;
return BinaryTreeTraversals.DepthFirstPostOrder(tree, fn);
}
private static NodeInfo ProcessNode(Node<uint> root, NodeInfo left, NodeInfo right)
{
// ...
}
}
}
The ProcessNode function is the meat of the solution. It will be called recursively for each node (sub-tree) in the tree. Each call will contain the following parameters: the root node of the current sub-tree and two NodeInfo objects representing the result of the calls to ProcessNode for the left and right child nodes respectively.
As with most recursive functions we need to identify the base case, for which we return the base result, and otherwise generate a result based on the state passed on the call stack. The logic for the latter case is as follows …
If the root value is greater than the root value for a given child then MaxIncPathLenToRoot through the new root will be one larger than that of the child. Conversely if the root value is less than the child root value then the new MaxDecPathLenToRoot will be one larger than that of the child. The final Max(Inc/Dec)PathLenToRoot values will be the larger of the results for the left and right children.
Then we need to update MaxPathLen. The new value will start out as the larger of MaxPathLen from the two children. Then we will check the new Max(Inc/Dec)PathLenToRoot values and take the larger of the two if it is larger than the current MaxPathLen. Finally we check for an up/down path through the current node, i.e. whether the current root value lies between the child root values, in which case we can calculate a new candidate MaxPathLen as the sum of the Max(Inc/Dec)PathLenToRoot values from the children plus one. If this value is greater than the current MaxPathLen then we use it.
Here’s the actual code …
namespace GinjaSoft.TreeStuff
{
public partial class LongestPath
{
private static NodeInfo ProcessNode(Node<uint> root, NodeInfo left, NodeInfo right)
{
// Base result for a leaf node
var returnValue = new NodeInfo {
RootValue = root.Value,
MaxIncPathLenToRoot = 1,
MaxDecPathLenToRoot = 1,
MaxPathLen = 1
};
// If there are no children to process then we are done
if(left == null && right == null) return returnValue;
// Process children ...
if(left != null) {
// Update the min/max PathLenToRoot based on the current root value and left child root value
if(root.Value > left.RootValue) returnValue.MaxIncPathLenToRoot = left.MaxIncPathLenToRoot + 1;
else if(root.Value < left.RootValue) returnValue.MaxDecPathLenToRoot = left.MaxDecPathLenToRoot + 1;
}
if(right != null) {
// Update the min/max PathLenToRoot based on the current root value and right child root value
if(root.Value > right.RootValue) {
var pathLen = right.MaxIncPathLenToRoot + 1;
returnValue.MaxIncPathLenToRoot = Math.Max(returnValue.MaxIncPathLenToRoot, pathLen);
}
else if(root.Value < right.RootValue) {
var pathLen = right.MaxDecPathLenToRoot + 1;
returnValue.MaxDecPathLenToRoot = Math.Max(returnValue.MaxDecPathLenToRoot, pathLen);
}
}
// The initial new MaxPathLen is the max of the children ...
var leftMaxPathLen = left != null ? left.MaxPathLen : 0;
var rightMaxPathLen = right != null ? right.MaxPathLen : 0;
returnValue.MaxPathLen = Math.Max(leftMaxPathLen, rightMaxPathLen);
// Take either of the two new max path lengths through the root if larger ...
returnValue.MaxPathLen = Math.Max(returnValue.MaxPathLen, returnValue.MaxIncPathLenToRoot);
returnValue.MaxPathLen = Math.Max(returnValue.MaxPathLen, returnValue.MaxDecPathLenToRoot);
// Now check for paths that go up and down through the root ...
if(left != null && right != null) {
if(root.Value > left.RootValue && root.Value < right.RootValue) {
var upDownPathLen = left.MaxIncPathLenToRoot + right.MaxDecPathLenToRoot + 1;
returnValue.MaxPathLen = Math.Max(returnValue.MaxPathLen, upDownPathLen);
}
else if(root.Value < left.RootValue && root.Value > right.RootValue) {
var upDownPathLen = left.MaxDecPathLenToRoot + right.MaxIncPathLenToRoot + 1;
returnValue.MaxPathLen = Math.Max(returnValue.MaxPathLen, upDownPathLen);
}
}
return returnValue;
}
}
}
Solution Validation
Let’s verify that our code will solve the example that we provided before …
namespace GinjaSoft.TreeStuff.Tests.LongestPathTests
{
using Xunit;
using Xunit.Abstractions;
public class GetNodeInfoTests
{
private readonly ITestOutputHelper _output;
public GetNodeInfoTests(ITestOutputHelper output)
{
_output = output;
}
[Fact]
public void ThroughPathDoesNotIncludeRoot()
{
// 10
// / \
// 30 40
// / \
// 40 20
// \
// 10
var tree = new Node<uint>(10) {
Left = new Node<uint>(30) {
Left = new Node<uint>(40) { },
Right = new Node<uint>(20) {
Right = new Node<uint>(10) { }
}
},
Right = new Node<uint>(40) { }
};
var nodeInfo = GetNodeInfo(tree);
Assert.Equal(10u, nodeInfo.RootValue);
Assert.Equal(1u, nodeInfo.MaxIncPathLenToRoot);
Assert.Equal(3u, nodeInfo.MaxDecPathLenToRoot);
Assert.Equal(4u, nodeInfo.MaxPathLen);
}
}
}
Woot! The test passes.
Resources
- GitHub repo with code and full unit test suite
