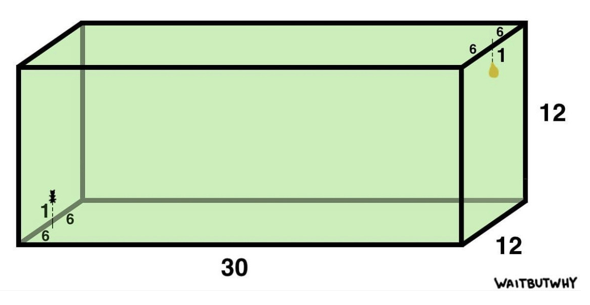
A Puzzle

I found this puzzle the other day, posted on Facebook by Wait But Why. It intrigued and entertained me, and so I wanted to share it here. Here’s the description …

“An ant is inside a box (see image above), 1cm from the bottom on the left face, and wants to go eat a drop of honey on the opposite side, 1cm from the top. Both the ant and the honey drop are exactly 6cm from the front and back walls. Crawling on the inside of the box, what’s the shortest distance the ant needs to travel to get to its prize?”

When presented with this most people start with a strategy like …

• Walk 1 cm down to the middle bottom of the left face
• Walk 30 cm across the middle of the bottom face
• Walk 11 cm up the right face
• Enjoy that lovely sweet honey dude

This makes for a total journey of 42cm. But this is not the shortest route, the ant can do better.

OK, how about some diagonals?

• Walk 6cm across the left face, parallel to the lower face, to get to a point 1cm up from the front, lower, left corner
• Walk diagonally across the front face to a point 1cm down from the front, top, right corner (\(\sqrt{30^2 + 10^2}\) cm)
• Walk 6cm across the right face, parallel to the lower face, to get to the honey
• Honey, nom, nom!

This makes for a total journey of \(12 + \sqrt{30^2 + 10^2} \approx 43.6\) cm. Hmm, that’s even longer.

This is all a bit random though, there must be a systematic way to think about this. Straight lines! The shortest distance between two points is a straight line. But that only works on “flat” surfaces. What’s a straight line on the inside of a box?

We need to transform our box into a flat surface. Let’s imagine that it was a real cardboard box so that we could cut it along some of its edges and then “unroll” it to get …

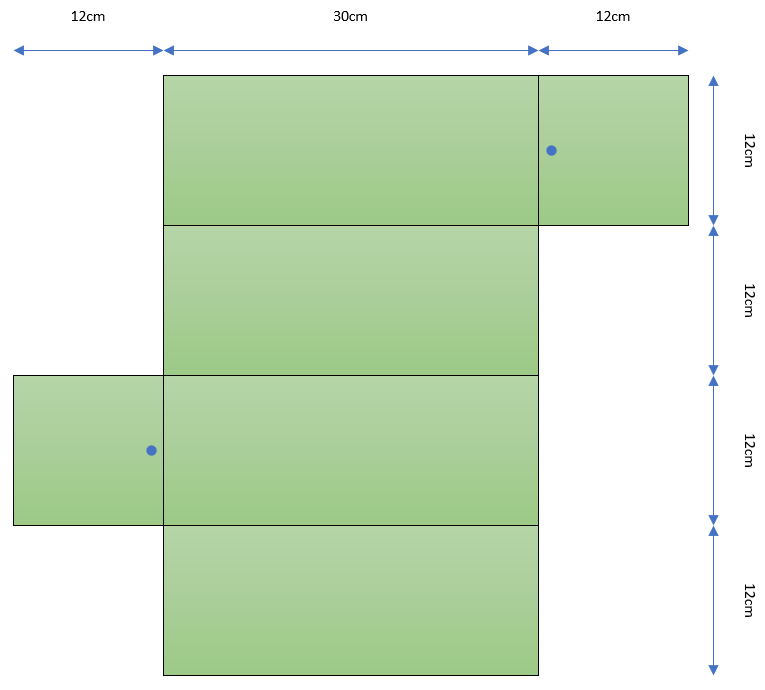
Aha! Now there is an obvious straight line path from the ant to the honey …

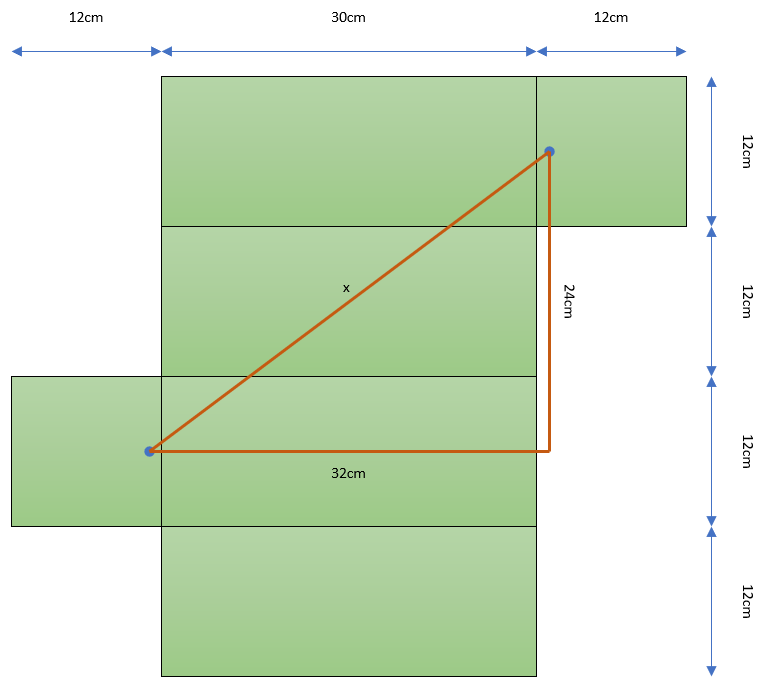
This path is \(\sqrt{32^2 + 24^2} = 40\) cm long. Better! And this is indeed the shortest path.

So what does this look like on the box? Well, it looks like this …

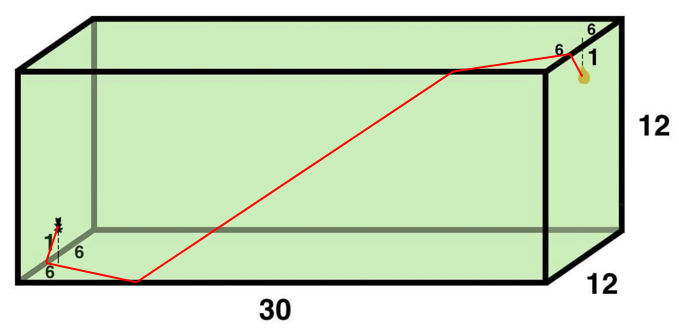
And how would we write down a description of the route? The strategy is essentially to “cut corners”, but exactly how much? We can easily calculate the coordinates of the way points, and then just tell the ant to walk in a straight line to each point in turn, but something tells me that he won’t really listen and will just do his own thing. There’s no telling these ants.

Anyway, I thought this was a neat little exercise that required some “outside of the box” thinking, pun very much intended.