Consider two right triangles: one with angles 45, 45 and 90 degrees; and another with angles 30, 60 and 90 degrees; both with a side of unit length. Via some Pythagoras and trig we can calculate the lengths of the other sides and everything turns out like this …

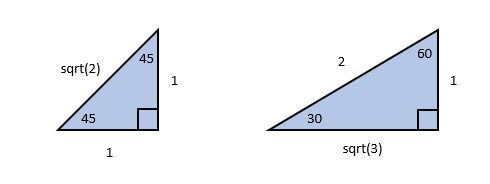
From this the values for the sine, cosine and tangent of the angles 30, 45 and 60 degress fall out and we can use the above diagram as an aide-mémoire for these common triganometric values.

\[\sin{45^\circ} = \frac{1}{\sqrt{2}}\] \[\cos{45^\circ} = \frac{1}{\sqrt{2}}\] \[\tan{45^\circ} = 1\] \[\sin{30^\circ} = \frac{1}{2}\] \[\cos{30^\circ} = \frac{\sqrt{3}}{2}\] \[\tan{30^\circ} = \frac{1}{\sqrt{3}}\] \[\sin{60^\circ} = \frac{\sqrt{3}}{2}\] \[\cos{60^\circ} = \frac{1}{2}\] \[\tan{60^\circ} = \sqrt{3}\]