The Pythagorean triganometric identity

$$\sin^2\theta + \cos^2\theta = 1$$

Proof:

In this right triangle …

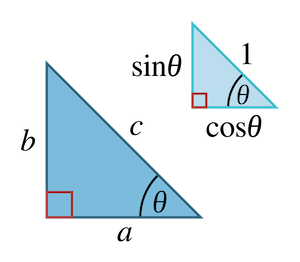
Pythagoras’ Theorem states that $a^2 + b^2 = c^2$. Dividing both sides by $c^2$ then gives us $\frac{a^2}{c^2} + \frac{b^2}{c^2} = 1$. Since the definitions of $\sin\theta$ and $\cos\theta$ are, respectively, $\frac{b}{c}$ and $\frac{a}{c}$, the above identity follows immediately.

QED.

Angle sum and difference identities

$$\sin(\alpha \pm \beta) = \sin\alpha\cos\beta \pm \cos\alpha\sin\beta$$ $$\cos(\alpha \pm \beta) = \cos\alpha\cos\beta \mp \sin\alpha\sin\beta$$ $$\tan(\alpha \pm \beta) = \frac{\tan\alpha \pm \tan\beta}{1 \mp \tan\alpha\tan\beta}$$

Proof:

Consider the following …

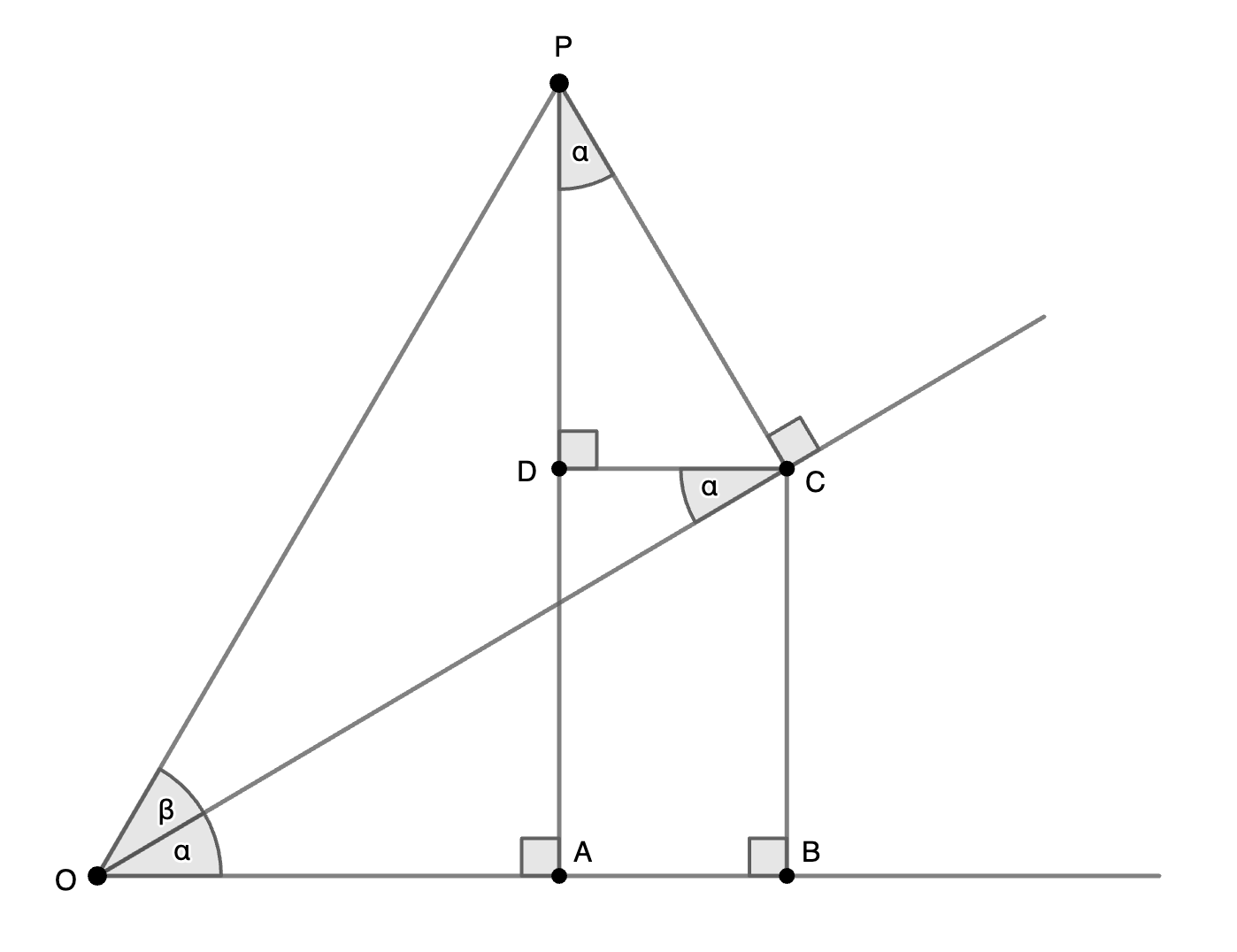
Here …

$$\sin\alpha = \frac{BC}{OC} = \frac{DC}{PC}$$ $$\sin\beta = \frac{PC}{OP}$$ $$\cos\alpha = \frac{OB}{OC} = \frac{DP}{PC}$$ $$\cos\beta = \frac{OC}{OP}$$ $$\sin(\alpha + \beta) = \frac{AP}{OP} = \frac{AD + DP}{OP} = \frac{BC + DP}{OP} = \frac{BC}{OP} + \frac{DP}{OP} = \frac{BC}{OC}\frac{OC}{OP} + \frac{DP}{PC}\frac{PC}{OP} = \sin\alpha\cos\beta + \cos\alpha\sin\beta$$ $$\cos(\alpha + \beta) = \frac{OA}{OP} = \frac{OB - AB}{OP} = \frac{OB - DC}{OP} = \frac{OB}{OP} - \frac{DC}{OP} = \frac{OB}{OC}\frac{OC}{OP} - \frac{DC}{PC}\frac{PC}{OP} = \cos\alpha\cos\beta - \sin\alpha\sin\beta$$

If we substitute $-\beta$ for $\beta$ in the above then we get …

$$\sin(\alpha + -\beta) = \sin\alpha\cos(-\beta) + \cos\alpha\sin(-\beta)$$ $$\cos(\alpha + -\beta) = \cos\alpha\cos(-\beta) - \sin\alpha\sin(-\beta)$$

But we know that $\cos(-\beta) = \cos\beta$ and $\sin(-\beta) = -sin\beta$ and so …

$$\sin(\alpha -\beta) = \sin\alpha\cos\beta - \cos\alpha\sin\beta$$ $$\cos(\alpha -\beta) = \cos\alpha\cos\beta + \sin\alpha\sin\beta$$

Now, since …

$$\tan\alpha = \frac{\sin\alpha}{\cos\alpha}$$

Then …

$$\tan(\alpha + \beta) = \frac{\sin(\alpha + \beta)}{\cos(\alpha + \beta)} = \frac{\sin\alpha\cos\beta + \cos\alpha\sin\beta}{\cos\alpha\cos\beta - \sin\alpha\sin\beta}$$

If we divide the top and bottom by $\cos\alpha\cos\beta$ then we get …

$$= \frac{\frac{\sin\alpha\cos\beta}{\cos\alpha\cos\beta} + \frac{\cos\alpha\sin\beta}{\cos\alpha\cos\beta}}{\frac{\cos\alpha\cos\beta}{\cos\alpha\cos\beta} - \frac{\sin\alpha\sin\beta}{\cos\alpha\cos\beta}}$$ $$= \frac{\frac{\sin\alpha}{\cos\alpha} + \frac{\sin\beta}{\cos\beta}}{1 - \frac{\sin\alpha\sin\beta}{\cos\alpha\cos\beta}}$$ $$= \frac{\tan\alpha + \tan\beta}{1 - \tan\alpha\tan\beta}$$

If we substitute $-\beta$ for $\beta$ in the above then we get …

$$\tan(\alpha + -\beta)= \frac{\tan\alpha + \tan(-\beta)}{1 - \tan\alpha\tan(-\beta)}$$

But we know that $\tan(-\beta) = -\tan\beta$ and so …

$$\tan(\alpha - \beta)= \frac{\tan\alpha - \tan\beta}{1 + \tan\alpha\tan\beta}$$

QED.