Given that my last post was about floating point I thought this comic strip was very apropos, and it also introduces the topic of \(\pi\) which is worth a post of its own.
So much has been written about \(\pi\) already, and it’s probably the most broadly known mathematical constant, but for those (hopefully few) who don’t know what it is I refer you to this button …

The ratio of the circumference of a circle to it’s diameter is a constant that is the same for any size circle. This constant has been known since antiquity and is represented by the greek letter \(\pi\) (pronounced pie). It is an irrational, and transcendental, number whose decimal representation is \(3.141592…\).
Now, why does the definition involve the diameter of the circle as opposed to the radius? This is a question around which there is some controversy and there are people who are firm believers that \(\pi\) is wrong and instead we should use the number \(6.283185…\) that they represent by the greek letter \(\tau\) (pronounced tau).
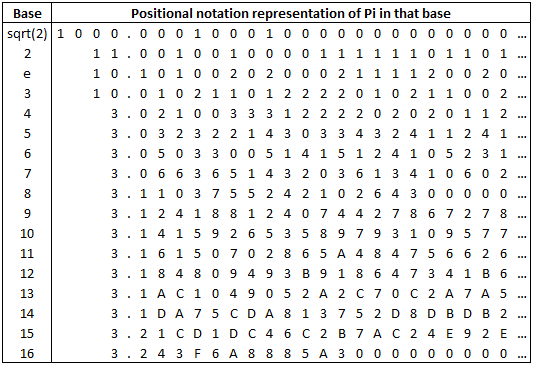
Most people can quote you the first few digits of \(\pi\) (\(3.141592…\)), and to many that “is” \(\pi\), but of course we know (as we learnt in my post about floating point it is but one possible representation, namely the base 10 positional notation representation. We can represent \(\pi\) in different bases as we can any number. Here are a few alternative representations:
Resources About \(\pi\)
- What Wikipedia has to say on the subject
- The Joy of Pi (the website that accompanied the book)
- A slice of Pi
- A million digits of Pi
- Vi Hart on Pi
- More Vi Hart on Pi
